Duration & Convexity: The Price/Yield Relationship
Investors who own fixed income securities should be aware of the relationship between a bond’s price and interest rates. As a general rule, the price of a bond moves inversely to changes in interest rates: a bond’s price will increase as rates decline and will decrease as rates move up. Macaulay duration is the weighted-average maturity of a bond’s cashflows, which is measured in years. Modified duration attempts to estimate how the price of a bond will change in response to a change in interest rates and is stated in terms of a percentage change in price. Typically when duration is quoted it is referring to a bond’s modified duration rather than Macaulay duration. Taking this concept one step further, a bond’s convexity is a measurement of how duration changes as yields change. These two measurements can provide insight into how a bond's price is expected to perform should interest rates change and can help investors understand the price risk of fixed income securities in different interest rate environments.
What is Duration?
In simple terms, modified duration gives an idea of how the price of a bond will be affected should interest rates change. A higher duration implies greater price volatility should rates move. Duration is quoted as the percentage change in price for each given percent change in interest rates. For example, the price of a bond with a duration of 2 would be expected to increase (decline) by about 2.00% for each 1.00% move down (up) in rates.
The duration of a bond is affected by its coupon rate, yield, and remaining time to maturity. The duration of a bond will be higher the lower its coupon. Duration will be higher the lower its yield. Duration will also be higher the longer its maturity. The following scenarios of comparing two bonds should help clarify how these three traits affect a bond’s duration:
- If the coupon and yield are the same, duration increases with time left to maturity
- If the maturity and yield are the same, duration increases with a lower coupon
- If the coupon and maturity are the same, duration increases with a lower yield
Example: Price/Yield Relationship for Bonds with Differing Maturities (5.00% coupon)
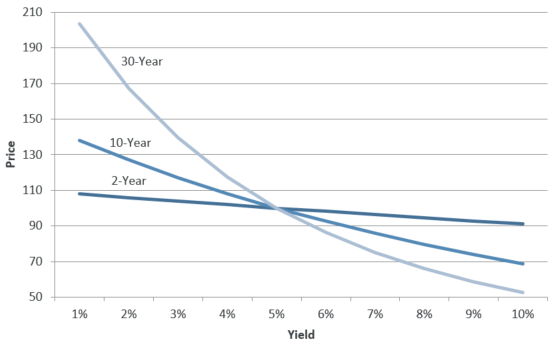
Example: 5.00% Coupon Bond at Par:
Price Change for a Given Rise in Rates
| If Rates Move Up ... | 2-Year Bond | 10-Year Bond | 30-Year Bond |
|---|---|---|---|
| 1.00% | -1.0% | -6.9% | -13.7% |
| 2.00% | -1.9% | -13.2% | -24.7% |
| 3.00% | -2.8% | -19.0% | -33.6% |
(Source: Raymond James)
These are hypothetical examples for illustrative purposes only. They are not intended to reflect the actual performance of any security.
Convexity:
As the yield on a bond changes so too does its duration. A bond’s convexity measures the sensitivity of a bond’s duration to changes in yield. Duration is an imperfect way of measuring a bond’s price change, as it indicates that this change is linear in nature when in fact it exhibits a sloped or “convex” shape. A bond is said to have positive convexity if duration rises as the yield declines. A bond with positive convexity will have larger price increases due to a decline in yields than price declines due to an increase in yields. Positive convexity can be thought of as working in the investor’s favor, since the price becomes less sensitive when yields rise (prices down) than when yields decline (prices up). Bonds can also have negative convexity, which would indicate that duration rises as yields increase and can work against an investor’s interest. The table below highlights the types of bonds that exhibit each type of convexity.
Examples of Bonds with Positive and Negative Convexity
| Type of Convexity | Typical Types of Bonds |
|---|---|
| Positive Convexity | Non-callable bonds, bonds with make-whole calls |
| Negative Convexity | MBS (most), bonds with a traditional call, preferreds |
(Source: Raymond James)
A useful way to visualize a bond’s convexity is to plot the potential price change against various yields. If two bonds have the same duration and yield but differing convexities, a change in interest rates will affect each bond differently. For example, the chart below shows three bonds: a bond with higher positive convexity (Bond A) will be less affected by interest rates than a bond with lower positive convexity (Bond B). On the other hand, a bond with negative convexity (Bond C) will exhibit larger price fluctuations should rates rise than if they were to fall.
Bonds Can Have Very Different Convexities: Positive vs. Negative
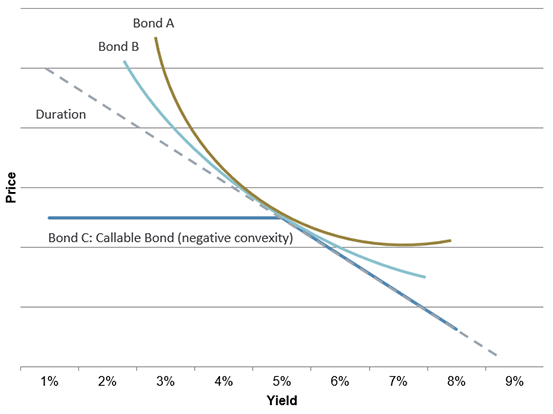
Conclusion:
Duration and convexity are two metrics used to help investors understand how the price of a bond will be affected by changes in interest rates. How a bond’s price responds to changes in interest rates is measured by its duration, and can help investors understand the implications for a bond’s price should interest rates change. The change in a bond’s duration for a given change in yields can be measured by its convexity.
- If rates are expected to increase, consider bonds with shorter durations. These bonds will be less sensitive to a rise in yields and will fall in price less than bonds with higher durations.
- If rates are expected to decline, consider bonds with higher durations. As yields decline and bond prices move up, higher duration bonds stand to gain more than their lower duration counterparts.